CBSE Class 10 Maths Notes Chapter 1 Real Numbers Pdf free download is part of Class 10 Maths Notes for Quick Revision. Here we have given NCERT Class 10 Maths Notes Chapter 1 Real Numbers. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.
CBSE Class 10 Maths Notes Chapter 1 Real Numbers
R = Real Numbers:
All rational and irrational numbers are called real numbers.
I = Integers:
All numbers from (…-3, -2, -1, 0, 1, 2, 3…) are called integers.
Q = Rational Numbers:
Real numbers of the form \(\frac { p }{ q }\), q ≠ 0, p, q ∈ I are rational numbers.
- All integers can be expressed as rational, for example, 5 = \(\frac { 5 }{ 1 }\)
- Decimal expansion of rational numbers terminating or non-terminating recurring.
Q’ = Irrational Numbers:
Real numbers which cannot be expressed in the form \(\frac { p }{ q }\) and whose decimal expansions are non-terminating and non-recurring.
- Roots of primes like √2, √3, √5 etc. are irrational
N = Natural Numbers:
Counting numbers are called natural numbers. N = {1, 2, 3, …}
W = Whole Numbers:
Zero along with all natural numbers are together called whole numbers. {0, 1, 2, 3,…}
Even Numbers:
Natural numbers of the form 2n are called even numbers. (2, 4, 6, …}
Odd Numbers:
Natural numbers of the form 2n -1 are called odd numbers. {1, 3, 5, …}
- Why can’t we write the form as 2n+1?
Remember this!
- All Natural Numbers are whole numbers.
- All Whole Numbers are Integers.
- All Integers are Rational Numbers.
- All Rational Numbers are Real Numbers.
Prime Numbers:
The natural numbers greater than 1 which are divisible by 1 and the number itself are called prime numbers, Prime numbers have two factors i.e., 1 and the number itself For example, 2, 3, 5, 7 & 11 etc.
- 1 is not a prime number as it has only one factor.
Composite Numbers:
The natural numbers which are divisible by 1, itself and any other number or numbers are called composite numbers. For example, 4, 6, 8, 9, 10 etc.
Note: 1 is neither prime nor a composite number.
I. Euclid’s Division lemma
Given two positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 ≤ r ≤ b.
Notice this. Each time ‘r’ is less than b. Each ‘q’ and ‘r’ is unique.

II. Application of lemma
Euclid’s Division lemma is used to find HCF of two positive integers. Example: Find HCF of 56 and 72 ?
Steps:
- Apply lemma to 56 and 72.
- Take bigger number and locate ‘b’ and ‘r’. 72 = 56 × 1 + 16
- Since 16 ≠ 0, consider 56 as the new dividend and 16 as the new divisor. 56 = 16 × 3 + 8
- Again, 8 ≠ 0, consider 16 as new dividend and 8 as new divisor. 16 = 8 × 2 + 0
Since remainder is zero, divisor (8) is HCF.
Although Euclid’s Division lemma is stated for only positive integers, it can be extended for all integers except zero, i.e., b ≠ 0.
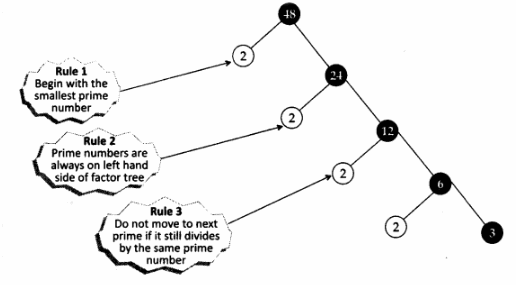
III. Constructing a factor tree
Steps
- Write the number as a product of prime number and a composite number
Example:
Factorize 48 - Repeat the process till all the primes are obtained
∴ Prime factorization of 48 = 24 x 3
IV. Fundamental theorem of Arithmetic
Every composite number can be expressed as a product of primes, and this expression is unique, apart from the order in which they appear.
Applications:
- To locate HCF and LCM of two or more positive integers.
- To prove irrationality of numbers.
- To determine the nature of the decimal expansion of rational numbers.
1. Algorithm to locate HCF and LCM of two or more positive integers:
Step I:
Factorize each of the given positive integers and express them as a product of powers of primes in ascending order of magnitude of primes.
Step II:
To find HCF, identify common prime factor and find the least powers and multiply them to get HCF.
Step III:
To find LCM, find the greatest exponent and then multiply them to get the LCM.
2. To prove Irrationality of numbers:
- The sum or difference of a rational and an irrational number is irrational.
- The product or quotient of a non-zero rational number and an irrational number is irrational.
3. To determine the nature of the decimal expansion of rational numbers:
- Let x = p/q, p and q are co-primes, be a rational number whose decimal expansion terminates. Then the prime factorization of’q’ is of the form 2m5n, m and n are non-negative integers.
- Let x = p/q be a rational number such that the prime factorization of ‘q’ is not of the form 2m5n, ‘m’ and ‘n’ being non-negative integers, then x has a non-terminating repeating decimal expansion.
Alert!
- 23 can be written as: 23 = 2350
- 52 can be written as: 52 = 2052
Class 10 Maths Notes
- Chapter 1 Real Numbers Class 10 Notes
- Chapter 2 Polynomials Class 10 Notes
- Chapter 3 Pair of Linear equations in Two Variables Class 10 Notes
- Chapter 4 Quadratic Equations Class 10 Notes
- Chapter 5 Arithmetic Progressions Class 10 Notes
- Chapter 6 Triangles Class 10 Notes
- Chapter 7 Coordinate Geometry Class 10 Notes
- Chapter 8 Introduction to Trigonometry Class 10 Notes
- Chapter 9 Some Applications of Trigonometry Class 10 Notes
- Chapter 10 Circles Class 10 Notes
- Chapter 11 Constructions Class 10 Notes
- Chapter 12 Areas related to Circles Class 10 Notes
- Chapter 13 Surface Areas and Volumes Class 10 Notes
- Chapter 14 Statistics Class 10 Notes
- Chapter 15 Probability Class 10 Notes